La
respuesta de un sistema, en estado estacionario, ante una entrada sinusoidal se
la conoce como respuesta en frecuencia. Interesa conocer la respuesta ante una entrada
sinusoidal ya que una señal real periódica será en general una poli armónica,
la que a su vez se podrá descomponer enseries de senos y cosenos donde se
tendrá en cuenta las funciones pares o impares, análisis de Fourier mediante,
luego si el sistema es lineal se analizarán las sinusoides por separado.
Sea
la siguiente entrada sinusoidal y su correspondiente transformada de Laplace:
La entrada x(t) es senoidal y se obtiene mediante: x(t) = X sen Ɯt
Si el sistema es estable, la salida y(t)se
obtiene a partir de: y(t) = Y sen( Ɯt +Φ)
En dónde:
Un sistema lineal e invariante con el tiempo se muestra en
la figura:
Un sistema estable, lineal e invariante con el tiempo,
sujeto a una entrada senoidal, tendrá, en estado estable, una salida senoidal
de la misma frecuencia que la entrada.
Un sistema estable, lineal e invariante con el tiempo, sujeto a una entrada senoidal, tendrá, en estado estable, una salida senoidal de la misma frecuencia que la entrada. Pero en general la amplitud y la fase de salida serán diferentes a las de la enrada.
En
esta imagen se muestra mejor las ondas de entrada y salida:
Es un sistema cuando esta excitado por una señal armónica de la forma r(t) = H senωt , donde H es la amplitud constante y ω la frecuencia angular de entrada, estando el sistema en estado estacionario. [1]
5.1.2 Especificaciones en el Dominio Frecuencial.
Se ha puesto de manifiesto anteriormente que la información que se busca en
el análisis de un sistema de control es normalmente la respuesta temporal.
Sin embargo, en general, la respuesta temporal es difícil de obtener
analíticamente a causa de la cantidad de cálculos que implica. Por
consiguiente, la respuesta frecuencial de un sistema de control se obtiene a
menudo por medio de métodos gráficos (representaciones polares y
rectangulares tales como los diagramas de Nyquist y Bode que se estudian
más adelante) y luego, la interpretación del comportamiento del sistema en el
dominio temporal se basa en las relaciones entre ambos dominios, temporal y
frecuencial. El punto de partida para el análisis en el dominio frecuencial es la función de
transferencia. Para un sistema de control con realimentación unitaria, la
función de transferencia de lazo cerrado es:
En condiciones de régimen sinusoidal, s = jω , la ecuación 29 se convierte en:
Cuando M ( jω) se escribe en forma de amplitud y fase, se tiene:
El significado de M ( jω) en un sistema de control es similar a la ganancia o
amplificación de un amplificador electrónico. En un amplificador de
audiofrecuencia, por ejemplo, el criterio ideal de proyecto es que el
amplificador tenga una curva de ganancia plana para las audiofrecuencias.
En
los sistemas de control, sin embargo, la situación ideal en algunas ocasiones
es que la salida siga a la entrada en todo instante o, simplemente, que el
módulo de M ( jω) sea igual a la unidad para todas las frecuencias. Pero en la
expresión de la ecuación 32 se ve que M ( jω) solo pede ser igual a la unidad
cuando G( jω) es infinito o, en otras palabras, la ganancia del sistema debe ser
infinita para todas las frecuencias. Esto es imposible de conseguir en la
práctica y además no es conveniente puesto que la mayoría de los sistemas
de control resultan inestables para valores elevados de ganancia. Además, todos los sistemas de control están sujetos a ruidos, es decir, además de
responder a la señal de entrada los sistemas deben ser capaces de rechazar y
suprimir los ruidos y las señales involuntarias. Esto significa que, en general,
la respuesta en frecuencia de un sistema de control debe de tener un punto de
corte característico y, algunas veces una banda pasante o no pasante
característica.
La característica de fase de la respuesta en frecuencia tiene también su
importancia. La situación ideal es que la fase sea una función lineal de la
frecuencia dentro de la banda de la señal de entrada. La figura 7 representa
las características de ganancia y de fase de un filtro pasa bajo ideal, imposible
de realizar físicamente. Las características típicas de amplitud y fase de un
sistema de control están dibujadas en la figura 7b. Se ve que la ganancia
disminuye al crecer la frecuencia. Ello es debido a los efectos de las inercias e
inductancias de los sistemas físicos, por lo que toda respuesta cesa cuando la
frecuencia tiende a infinito.
Las especificaciones más usadas de las características de un sistema de
control en el dominio frecuencial son las siguientes;
1- Ancho de banda. El ancho de banda, A. B., se define como la frecuencia a
la cual el módulo de M ( ) jω vale el 70.7 % del nivel a frecuencia cero o 3 dB
por debajo del nivel de frecuencia nula (figura 8). En general, el ancho de
banda indica les características de filtraje de ruido del sistema. El ancho de
banda da, también, una mecida de las propiedades de la respuesta transitoria.
Un ancho de banda largo indica, normalmente, que las señales de alta
frecuencia pasarán a la salida. Es decir, la respuesta transitoria debe de tener
un tiempo de subida rápido acompañado de un amplio rebase. Por el contrario, si el ancho de banda es chico, solo pasarán las señales de
baja frecuencia; por consiguiente, la respuesta temporal será lenta.
2- Factor de resonancia ( Mr ). Se define como el valor máximo de M ( ) ω ,
que proporciona además indicación de la estabilidad relativa del sistema. Si se
recuerda la figura 10 y como se verá más adelante, cuando se estudió el
diagrama de Bode de un sistema de segundo orden se obtienen distintas curvas de respuesta para distintos valores de δ .Es evidente que a valores
elevados de Mr corresponden amplios rebases de la respuesta temporal.
Cuando se proyecta se admite, generalmente, que el valor oprimo de Mr debe
estar comprendido entre 1.1 y 1.5.
3 — Frecuencia de resonancia (ωr ). Es la frecuencia para la que se produce
el factor de resonancia.
4 - Razón de corte. A menudo para frecuencias elevadas es importante la
razón de corte de la curva de respuesta, en frecuencia, puesto que indica la
capacidad del sistema para distinguir la señal de ruido. Sin embargo, las
características de corte agudo sen acompañadas normalmente de valores
elevados de Mr , lo que significa que el sistema es poco estable.
5 - Margen de amplitud y Margen de fase. Estas dos cantidades que son
una medida de la estabilidad relativa de un sistema. Serán definidos más
adelante cuando se estudien los diagramas de Bode y Nyquist.
5.1.3 - Especificaciones En El Dominio Frecuencial Para Un Sistema De
Segundo Orden
En un sistema de segundo orden, el factor de resonancia Mr y la frecuencia
de resonancia ωr depender, únicamente riel coeficiente de amortiguamiento δ
y de la frecuencia natural sin amortiguamiento ωn del sistema. Si se considera
la función de lazo cerrado de segundo orden:
Al utilizar la frecuencia reducida u = ω / ωn , el módulo de M ( jω) toma la
expresión:
Y la fase de M ( jω ) :
La frecuencia de resonancia se determina derivando M ( u ) con respecto a u e
igualando a cero, es decir: De donde:
Por consiguiente:
Y
La solución dada en la ecuación 39 indica meramente que la pendiente de la
curva M (ω) vale cero para ω = 0 0; no es un máximo. De la ecuación 40 se
obtiene la frecuencia de resonancia que vale:
Evidentemente, la ecuación 41 es válida solamente para 2 1 ≥ 2δ o δ ≤ 0.707 ,
puesto que de otra manera ωr sería imaginario. Esto significa simplemente
que para todos los valores de δ > 0.707
no hay resonancia (o = 1 M r ) en la
curva M (ω) en función de ω .
La curva M (ω) es inferior a uno para todos los
valores de ω > 0 si el coeficiente de amortiguamiento es mayor que 0.707 Sustituyendo la ecuación 40 en la 36a y simplificando se obtiene:
Es importante observar que Mr es función de
δ solamente, mientras que ωr
es función de ω y
δ .
Las figuras 9 y 10 representan respectivamente las
curvas de M r y de r u en función de δ .
En resumen se observa que a medida que el factor de amortiguamiento δ
tiende a cero, la frecuencia de resonancia tiende a ωr . Para 0 < δ < 0.707 , la
frecuencia de resonancia ωr es menor que la frecuencia natural con amortiguamiento "2 ωn = ωd 1− δ ", que aparece en la respuesta transitoria. Para
δ > 0.707 no hay pico resonante, la amplitud de G( jω) decrece
monótonamente cuando la frecuencia ω crece. Esto significa que no hay pico
en la curva de respuesta para δ > 0.707 (La amplitud es menor que 0 dB para
todos los valores de ω > 0 . Debe recordarse que para 0.707 < δ < 1, la respuesta
escalón es oscilatoria, pero las oscilaciones son muy bien amortiguadas y
apenas perceptibles.
Cuando δ tiende a cero M r tiende a infinito. Esto significa que si el sistema
no amortiguado es excitado a su frecuencia natural, la magnitud de G( jω) se
hace infinito.
Se puede obtener el ángulo fase de G j (ω) , a la frecuencia que se produce el
pico de resonancia.
Gráficas Polares.
Como se había mencionado anteriormente, para varios valores de ω se obtienen
los valores de M (ω) y φ(ω) los que podían ser graficados en coordenadas polares
o rectangulares. Se verá a continuación la primera de estas formas de
representación frecuencial.
El diagrama polar de una función de transferencia senoidal G( jω) es un diagrama
de la amplitud de G( jω) en función del ángulo de G( jω) en coordenadas polares al
variar ω desde cero a infinito.Se hace notar que en los diagramas polares, se
mide un ángulo 'de fase positivo (negativo) en sentido antihorario (en sentido
horario) desde el eje positivo real. En la figura 11 hay un ejemplo de ese diagrama.
Cada punto del diagrama polar de G( jω) representa el punto terminal de un
vector pera un valor determinado de ω. En el diagrama polar es importante
mostrar la graduación de frecuencia sobre el diagrama. Las proyecciones de G( jω)
en los ejes real e imaginario son sus componentes real e imaginario.Tanto la
amplitud G( jω) como el ángulo de fase G j ( ω) deben ser calculados directamente
para cada frecuencia ω para poder construir los diagramas polares. Sin embargo,
como el diagrama rectangular logarítmico que se verá posteriormente es fácil de
construir, la información necesaria para trazar el diagrama polar puede ser
obtenida directamente del diagrama logarítmico si se dibuja previamente aquél y
se convierte decibeles en una magnitud ordinaria usando la figura 33.

Pera dos sistemas conectados en cascada la función de transferencia total de la
combinación, en ausencia de efectos de carga, es el producto de las dos
funciones de transferencia individuales. Si se necesita la multiplicación de dos
funciones de transferencia senoidales, esta puede lograrse multiplicando las funciones de transferencia senoidales en cada frecuencia realizando la multiplicación
con álgebra compleja.
En la figura 12 se muestra el producto de G1 ( jw). G2( jw):
Una ventaja de usar un diagrama polar es que presenta las características de
respuesta de frecuencia de un sistema en todo el rango de frecuencias en un único
diagrama. Una desventaja es que el diagrama no indica claramente las
contribuciones de cada uno de los factores individuales de la función de transferencia de lazo abierto.
El diagrama polar de G( jω) = 1 es el eje imaginario negativo, pues:
El diagrama polar de G( jω) = jω es el eje positivo imaginario, pues:
5.1.5 - Factores de Primer Orden.
Para la función de transferencia senoidal:
Los valores de G( jω) en ω = 0 y ω = 1/T son respectivamente:
Al tender ω a infinito:
El diagrama polar de esta función de transferencia es una semicircunferencia al
variar la frecuencia desde cero a infinito, como se ve en la figura 13a. El centro
está ubicado en 0.5 sobre el eje real y el radio es igual a 0.5.
Para probar que el diagrama polar es una semicircunferencia se define:
Dónde:
Entonces se obtiene:
Entonces en el plano x-y, G( jω) es un círculo con centro en X=1/2; Y=0 y
con un radio igual a 1/2 como puede verse en la figura 13b. La
semicircunferencia inferior corresponde a 0 ≤ ω ≤ ∞ y la semicircunferencia
superior corresponde a − ∞ ≤ ω ≤ 0 . El diagrama polar de la función de transferencia 1+ jωT es simplemente la
mitad superior de la línea recta que pasa por el punto (1,0) en el plano
complejo y paralelo al eje imaginario, como puede verse en la figura 14.
5.1.6 - Factores cuadráticos
Las porciones de alta y baja frecuencia del diagrama polar de la función
de transferencia senoidal siguiente:
Están dadas respectivamente por:
El diagrama polar de esta función de transferencia senoidal comienza en
1 |0º y finaliza en 0 |-180º al aumentar ω desde cero a infinito.
Así, la porción alta frecuencia de G(jω) es tangente al eje real negativo.
Los valores de G ( j ω) en el rango de frecuencias de interés pueden ser
catalogados directamente.
En la figura 15, hay ejemplos de diagramas polares de la función de transferencia recién analizada. La forma exacta de un diagrama polar depende del
valor de la relación de amortiguamiento δ , pues la forma general es la
misma, tanto para el caso subamortiguado ( 0 1 < δ < ) como para el caso
sobreamortiguado (δ >1).
Para el caso sobreamortiguado, cuando δ es bastante mayor que la unidad
el lugar de G j ( ) ω se aproxima a una semicircunferencia. Se puede ver esto
del hecho de que para un sistema fuertemente amortiguado, las raíces
características son reales y es una mucho más pequeña que la otra. Como
para un valor de δ suficientemente grande el efecto de la raíz más grande
en la respuesta se hace muy pequeña, el sistema se comporta como un
sistema de primer orden.
Para la función de transferencia senoidal:
La porción de baja frecuencia de la curva es:
Y la porción de alta frecuencia es:
Como la parte imaginaria de G (jω) es positiva para ω > 0 y es
monótonamente creciente; la parte real de G j( jω) es monótonamente
decreciente desde la unidad, la forma general del diagrama polar de G ( jω) de la ecuación 60a es como puede verse en la figura 17.
El ángulo de fase está entre 0° y 180°.
5.1.7 - Retardo de transporte.
Algunos elementos en los sistemas de control se caracterizan por su tiempo
muerto o retraso de transporte, durante el cual no dan salida a la señal de
entrada que se les haya aplicado; hay un periodo muerto de inactividad que
demora la transmisión de la señal recibida. La figura 19 muestra el
diagrama de bloques del elemento demorador:
La demora es una característica
no lineal que, afortunadamente, puede ser representada por su
transformada de Laplace. Así:
Puede ser escrito:
Como el módulo G (jω) es simple la unidad y el ángulo de fase varía
linealmente con ω , el diagrama polar del retardo de transporte es un círculo
de radio unitario, como puede verse en la figura 21.

A frecuencias bajas, el retardo de transporte j T e− ω y el retardo de primer
orden 1/ (1 + jωT ) se comportan en forma similar, lo que puede verse en la
figura 22.
A continuación se anexan unos vídeos de la plataforma YouTube con fines educativos, para reforzar lo aprendido en este subtema, sobre el análisis y simulación en la frecuencia de los sistemas lineales que no tienen variación en el tiempo (LTI), así como un ejemplo en el software MATLAB.
|
| K. Ogata, Análisis y Simulación en la frecuencia de
sistemas lineales invariantes en tiempo, Estado de Mexico: Prentice all,
2004. http://dea.unsj.edu.ar/control1b/AnalisisFrecuencial.pdf
|
|
|
|
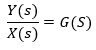



















































Comentarios
Publicar un comentario